Dil dediğin nedir ki?

Dil dediğin nedir ki?

“Eğer derleyicilerin (compiler) ya da yorumlayıcıların (Interpreter) nasıl çalıştığını bilmiyorsanız, bilgisayarın nasıl çalıştığını bilmiyorsunuz. Eğer derleyici veya yorumlayıcıların nasıl çalıştığını %100 bilmiyorsanız o zaman bunların nasıl çalıştığını kesinlikle bilmiyorsunuz.

- Steve Yegge

Son birkaç senede hayatımda değişik tecrübeler etme şansım oldu, bu tecrübeler her ne kadar beni sosyal olarak farklı noktalara taşısalar da aslında düşünce olarak da farklı noktalara taşıdılar.

Bir mühendis adayı olarak her ne kadar bilgisayarları ve onların işleyişini sevsem de günden güne bu işleyişi daha da soyutlaştığımızı düşünmekteyim. Programcılar olarak tekrar etmekten korktuğumuz ve hayatımızı kolaylaştırmak için yarattığımız uygulamaları daha da soyutlaştırdığımız, ana probleme odaklanmaktansa kendimize yeni problemler yarattığımız XY Problemi bir dünyaya girdiğimizi düşünüyorum. Örneğin basit bir SQL querysi yazmaya bile üşeniyoruz ve bunun için bile bir script veya bir paket yazıyoruz ya da kullanıyoruz. Bunun açıkçası bizi geliştirmekten ziyade müşteri konumuna attığını düşünüyorum. Birileri gerçekten geliştiriyor ve biz kullanıyoruz, nasıl çalıştığını bilmeden. Bunu kendi içimde kırmayı amaçlıyorum, bundan dolayı bu yazıyı yazıyorum.

Herkesin hayatında eminim ki “şunu da yapsam iyi olur” dediği şeyler vardır, kendi dilimi yazma ve kendi bilgisayarımı yapma benim için biraz böyle, yapmam gerektiği için değil yapmak istediğim için yaptığım şeylerden. Uzun zaman sonra bunun hakkında yazmak istiyorum. Yazmak istiyorum ki yazarken öğreniyim ve bunu aktarayım. Kendimizi bilgimizi aktardıkça var ederiz.

Bu yazıda aslında temel olarak toplama ve çıkarma işlemlerini yapabilen bir yorumlayıcı (Interpreter) tasarlayacağız, çok derinlemesine olmayacak tabii ki ancak başlangıç için uygun olacaktır.

Her şeyin başlangıcı

Burası işin biraz teorik tarafı, kendi bilgilerimi Automata teorisi hakkında bilgilerimi tazelemem gerekti.

^{(Bu kısımda biraz daha bilgi sahibi olmak için aşağıda bazı linkler bırakacağım.)}

1. Context Free Languages

Tabii ki de bu bir sihir değil. Şu anda kullandığımız çoğu diller Temelde bu şekilde çalışıyor. Bu diller bazı kurallara bağlı. Örneğin

S -> S + F | S - F | F
F -> N

Bu dil aşağıda bahsedeceğimiz ekleme çıkarma operasyonlarımızı sağlayan bir dil.

S -> Expression => Aritmetik operasyonun adı örneğin 2 + 3 + 4 + 5.

F -> Factor => En temel yapı taşı sayı veya daha kompleks şeyler olabilir.

Gelin bu dili JFLAP üzerinde yazalım;

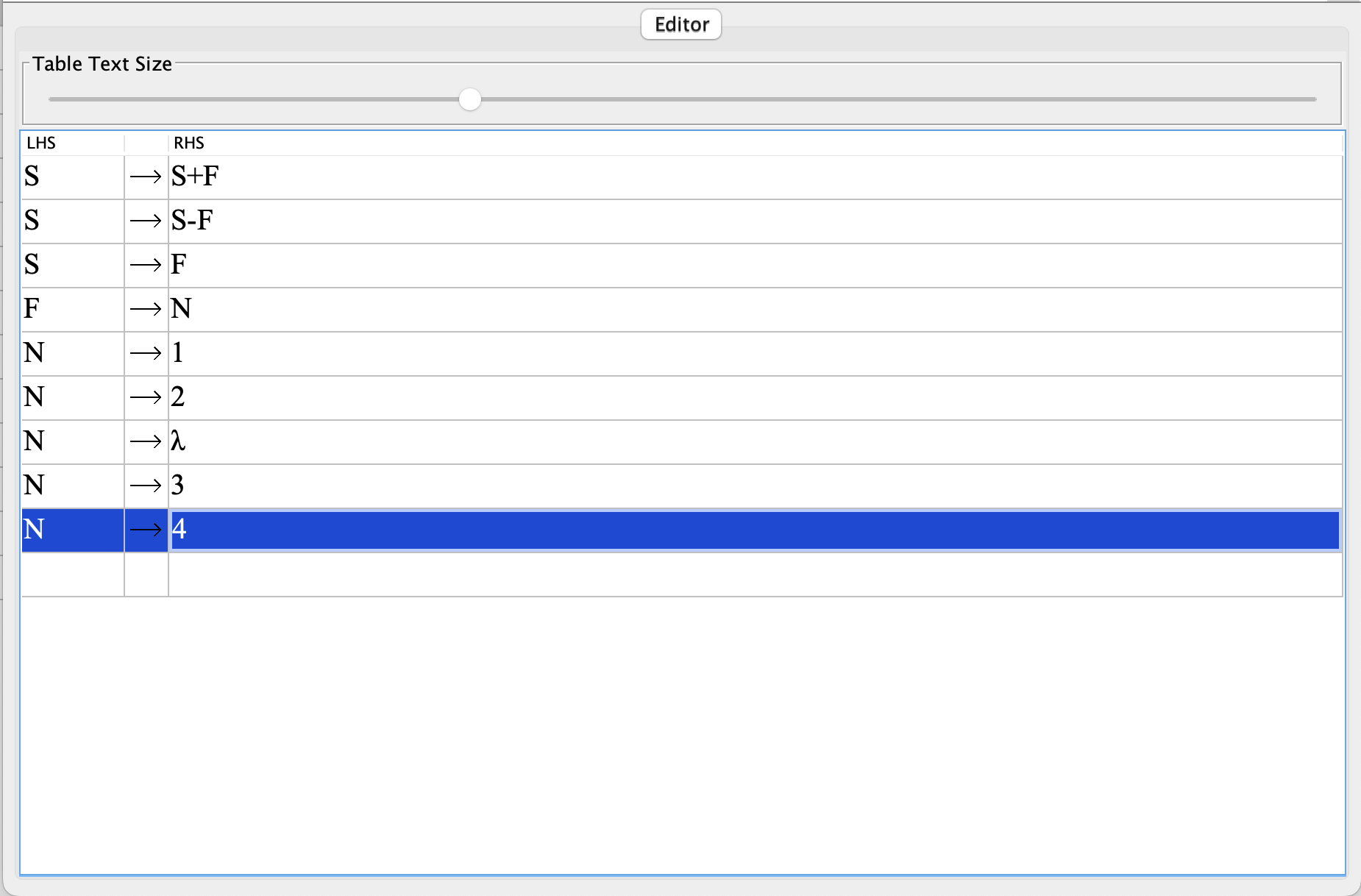
Dilimiz o kadar basit bir dil ki sayılar arasındaki boşlukları dahi kabul etmiyor örneğin 1 + 3 + 4 doğru bir yazım değil bunun yerine 1+3+4 yazmalıyız.

Bir JFLAP örneği;

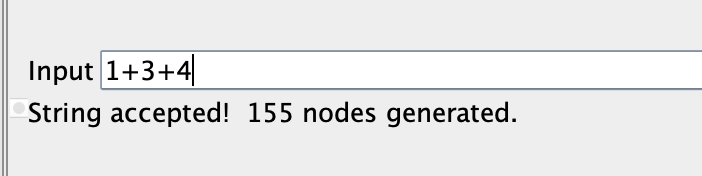
Rakamları toplamak bana açıkçası çok ilgi çekici gelmedi, bir aritmetik işlem yapacaksak bunun rakamlardan daha kalifiye olmasını beklerim, en azından sayıları toplayabilelim.

Bunun için kurallarımızda bir değişikliğe gitmeliyiz.

S -> S + F | S - F | F
-----------
| F -> NF | ∈
-----------

Bu sayede N kendisini tekrar çağırabilir ve birden çok basamaklı sayı üretebilir.

Yeni kurallarımızla tekrar JFLAP Brute Force Parserimizi deneyelim;

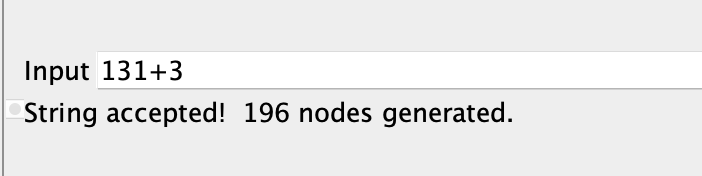
Verdiğimiz metin kabul edildi! Dilimiz çalışıyor. ANCAK bir sorun var. Belirsizlik.

1.1 Ambiguity

Literatür ismi Ambiguity olan Türkçe’ye belirsizlik olarak çevirebileceğimiz bir durum söz konusu oldu burada.

Bunun detaylarına girmeden bu konuyu daha iyi anlayabilmeniz için öncelikle size bilgisayarların deterministik bir cihaz olduğunu söylemem gerekiyor. Deterministik sistem inceleme ise bu sistemde rastgelelik bulunmayan sistem demek kısaca. Yani bilgisayar rastgele çalışmıyor.

E peki konumuz ile alakası ne?

Gelin dilimizi biraz inceleyelim;

Varsayalım şu şekilde 1+2+3 bir toplama işlemi yapacaksak, gelin bunu beraber yorumlayalım:

İlk aşamada S kuralımızı koymalıyız, her şeyin başı kendisi. Bildiğiniz üzere S 3 farklı kurala gidebiliyor: S+F | S-F | F. Bunlardan hangisini koymalıyız? Unutmayın sadece 1 rakamına bakıyoruz şu an. Evet sizi duyar gibiyim sadece 1 rakamına bakarak hangisini koymamız gerektiğini anlamamız mümkün değil. Bunun için dilimizi biraz sadeleştirmemiz gerekiyor.

Ne dedik? Bilgisayarlar deterministik dedik ve rastgele çalışamazlar dedik ancak şu anda bir rastgelelikten bahsediyoruz. Bu da Ambiguity Türkçesiyle Belirsizlik yaratiyor. Dilimizi implemente etmeden önce yapmamız gereken son bir adım kaldı o zaman.

1.2 Belirli Dile Çevirme

Bunlardan kurtulmanın çok basit aşamaları var, ancak unutmamak gerekir ki eğer yarattığınız dil varoluşsal olarak belirsizlik yaratıyorsa bu aşamaları yapmak sizi bu durumdan kurtarmayabilir, bizim dilimizde böyle bir sorun mevcut değil.

S -> FS'
S' -> +FS'
S' -> -FS'
F -> F'
F -> NF'
F' -> ∈
N -> 1 | 2 | 3 | 4 | 5 | ...

Tam şu an bu noktada dilimiz hazır diyebiliriz. Dilerseniz JFLAP üzerinden kontrol edelim.

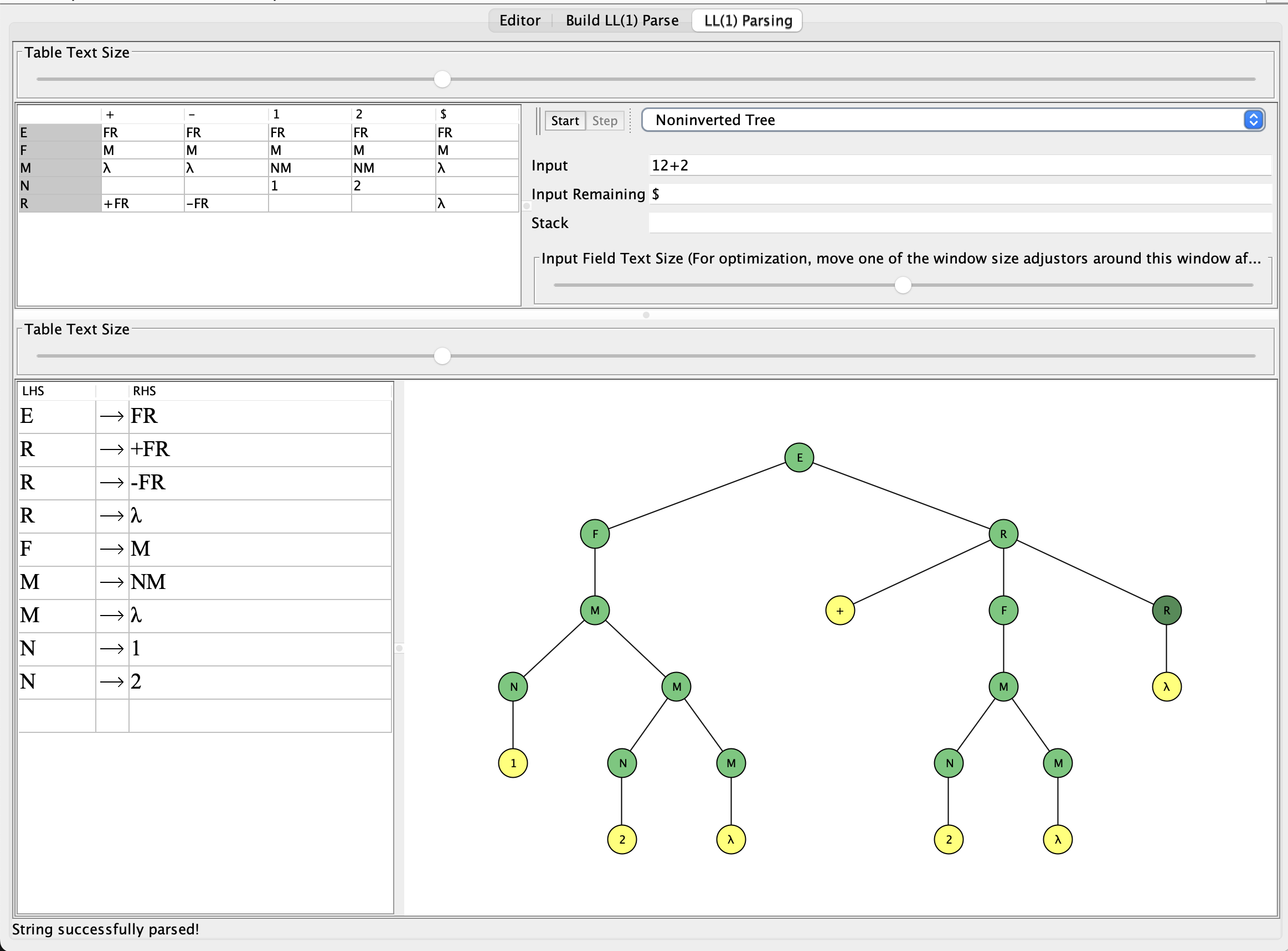
Bu sekmede JFLAP üzerinden Grammer olarak erişebilirsiniz, buranın çok fazla detayına girip kafanızı bulandırmak istemiyorum.

2 Parsing

Tabii ki de bu şekilde yazmamız bilgisayarımız için bir anlam ifade etmiyor. Bunu bir şekilde küçük parçalara ayırıp programlayabileceğimiz hale getirmemiz gerekiyor.

2.1 Tokenizer

İlk başta Tiplerimizi (TYPE) tanılayalım.

TYPE_INTEGER = "INTEGER"
TYPE_PLUS = "PLUS"
TYPE_MINUS = "MINUS"
TYPE_EOF = "EOF"

Token Sınıfımız sayesinde gelen verimizi sınıflandırabileceğiz. Ancak eğer elimizde bunu yorumlayacak bir yorumlayıcı olmaz ise ne işe yarar bu yazdığımız Tokenizer? Bu noktada durup da kendi Lexer/Tokenizerinizi yazmayı düşünebilirsiniz. Yapmanız gereken tek şey gelen karakterlerin tokenlarını yaratmak artından bunları bir sonuca yazmak olmalı değil mi? Yine de sizin aklınızı bulandırmamak için Lexer sınıfı;

class Lexer:
    def __init__(self, text):
        self.text = text
        self.pos = 0
        self.current_token = None
        self.current_char = self.text[self.pos]

    def error(self):
        raise Exception('Error While Parsing')

    
    # Bir sonraki poziyona gecmek icin gereken fonksiyon.
    #
    def advance(self):
        self.pos += 1
        if self.pos > len(self.text) - 1:
            self.current_char = None
        else:
            self.current_char = self.text[self.pos]

    # `eat` ya da `consume` olarak gorebileceginiz
    # degerimizi verdigimiz type ile eslestigi takdirde
    # yiyen bir fonksiyon.
    #
    def eat(self, type):
        if self.current_token.type == type:
            self.current_token = self.get_next_token()
        else:
            self.error()

    # Birden cok basamakli sayilarla islem yapmak icin
    # gereken fonksiyon. 
    #
    def make_number(self):
        number = ''
        while self.current_char is not None and self.current_char.isdigit():
            number += self.current_char
            self.advance()
        return number

    # Siradaki Tokenimizi yaratana fonksiyonumuz.
    #
    #
    def get_next_token(self):
        
        while self.current_char is not None:
            if self.current_char.isdigit():
                number = self.make_number()
                return Token(TYPE_INTEGER, int(number))
            if self.current_char == '+':
                self.advance()
                return Token(TYPE_PLUS, None)
            if self.current_char == '-':
                self.advance()
                return Token(TYPE_MINUS, None)

            self.error()

        return Token(TYPE_EOF, None)

    # Kurallarda da yaptigimiz gibi Factor (F) kuralimizi
    # temsil eden fonksiyonumuz.
    #
    def factor(self):
        if self.current_token is not None and self.current_token.type == TYPE_INTEGER:
            value = self.current_token.value
            self.eat(TYPE_INTEGER)
            return value

    # Kurallarda oldugu gibi Expression (E) kuralimizi
    # temsil eden fonksiyonumuz.
    #
    def expr(self):
        self.current_token = self.get_next_token()

  
        result = self.factor()

        while self.current_token.type is not None and self.current_token.type is not TYPE_EOF:
            
            op = self.current_token
            if op.type == TYPE_PLUS:
                self.eat(TYPE_PLUS)
            elif op.type == TYPE_MINUS:
                self.eat(TYPE_MINUS)


            if op.type == TYPE_PLUS:
                result += self.factor()
            elif op.type == TYPE_MINUS:
                result -= self.factor()

            
        return result
 

Tekrar dilimizin kurallarını gözden geçirelim:

• Dilimiz boşlukları kabul etmiyor (3 + 3) geçerli değil.
• Dilimiz birden fazla basamaklı sayıyı kabul ediyor (13+3).
• Dilimiz sadece toplama ve çıkarma işlemini yapabiliyor.

Görüldüğü üzere kurallarımıza gayet sadık şekilde bir kod yazdık. Şimdi kullanıcıdan değerleri alıp bunları dilimize atacak basit bir kod yazalım.

from interpreter import Lexer


def main():
    while True:
        text = input('mylang> ')
        interpreter = Lexer(text)
        result = interpreter.expr()
        print(result)

if __name__ == '__main__':
    main()

Simdi deneyelim:

Gördüğünüz gibi çalışıyor!

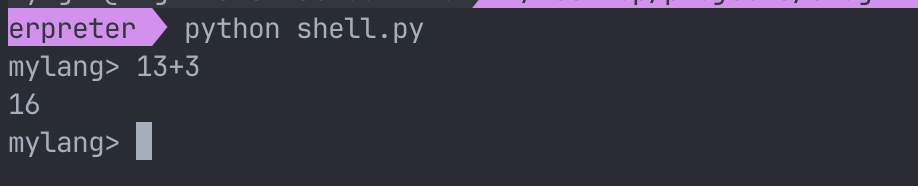
Eğer bu konuda devam etmek isterseniz, işte bu koda ekleyebileceğiniz/değiştirebileceğiniz birkaç özellik:

• Toplama ve çıkarma yerine operasyonları çarpma ve bölme yapmaya ayarlayın.
• Boşluk karakterlerini destekleyin, örneğin 13+3 ve 13 + 3 desteklensin.
• Bakmadan tekrar kodu, rahat olduğunuz bir dille yazmaya çalışın.

Kaynakca

• Pragmatic Programmers, (2010), Terrence Parr
• Writing Compilers and Interpreters_ A Software Engineering Approach, (2009), Ronald Mak
• Ruslan’s Blog
• JFLAP